Difference in Differences with pymc models

Note

This example is in-progress! Further elaboration and explanation will follow soon.

import arviz as az

import causalpy as cp

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
seed = 42

Load data

df = cp.load_data("did")
df.head()

	group	t	unit	post_treatment	y
0	0	0.0	0	False	0.897122
1	0	1.0	0	True	1.961214
2	1	0.0	1	False	1.233525
3	1	1.0	1	True	2.752794
4	0	0.0	2	False	1.149207

Run the analysis

Note

The random_seed keyword argument for the PyMC sampler is not necessary. We use it here so that the results are reproducible.

result = cp.DifferenceInDifferences(
    df,
    formula="y ~ 1 + group*post_treatment",
    time_variable_name="t",
    group_variable_name="group",
    model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]

fig, ax = result.plot()

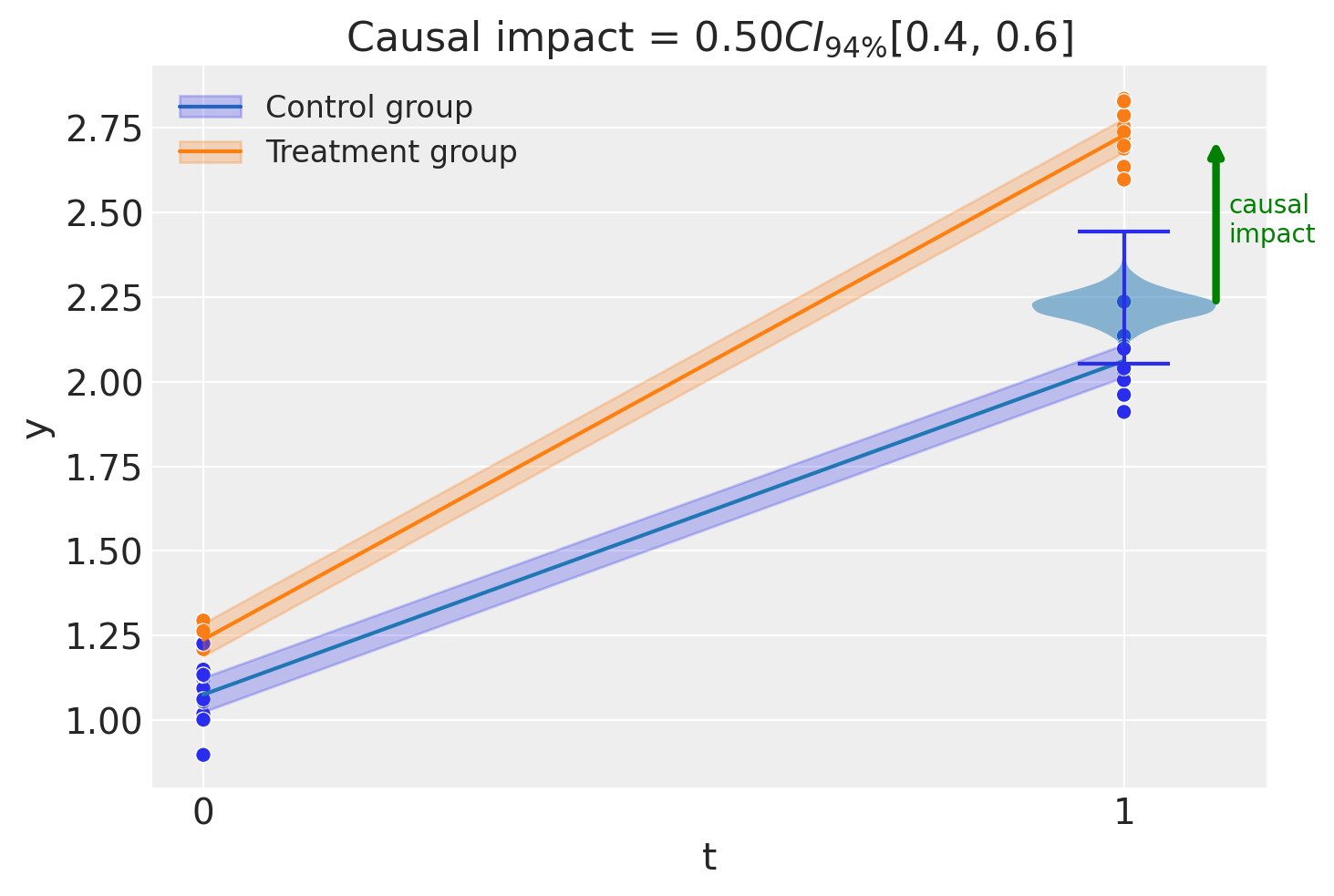
result.summary()

===========================Difference in Differences============================
Formula: y ~ 1 + group*post_treatment

Results:
Causal impact = 0.50$CI_{94\%}$[0.4, 0.6]
Model coefficients:
    Intercept                     1.1, 94% HDI [1, 1.1]
    post_treatment[T.True]        0.99, 94% HDI [0.92, 1.1]
    group                         0.16, 94% HDI [0.094, 0.23]
    group:post_treatment[T.True]  0.5, 94% HDI [0.4, 0.6]
    y_hat_sigma                   0.082, 94% HDI [0.066, 0.1]

ax = az.plot_posterior(result.causal_impact, ref_val=0)
ax.set(title="Posterior estimate of causal impact");

Effect Summary Reporting

For decision-making, you often need a concise summary of the causal effect. The effect_summary() method provides a decision-ready report with key statistics. Note that for Difference-in-Differences, the effect is a single scalar (average treatment effect), unlike time-series experiments where effects vary over time.

# Generate effect summary
stats = result.effect_summary()
stats.table

	mean	median	hdi_lower	hdi_upper	p_gt_0
treatment_effect	0.503779	0.504367	0.401661	0.607651	1.0

print(stats.text)

The average treatment effect was 0.50 (95% HDI [0.40, 0.61]), with a posterior probability of an increase of 1.000.

You can customize the summary with different directions and ROPE thresholds:

• Direction: Test for increase, decrease, or two-sided effect

• Alpha: Set the HDI confidence level (default 95%)

• ROPE: Specify a minimal effect size threshold

# Example: Two-sided test with ROPE
stats = result.effect_summary(
    direction="two-sided",
    alpha=0.05,
    min_effect=0.3,  # Region of Practical Equivalence
)
stats.table

	mean	median	hdi_lower	hdi_upper	p_two_sided	prob_of_effect	p_rope
treatment_effect	0.503779	0.504367	0.401661	0.607651	0.0	1.0	0.99925

print("\n" + stats.text)

The average treatment effect was 0.50 (95% HDI [0.40, 0.61]), with a posterior probability of an effect of 1.000.