Excess deaths due to COVID-19

import pandas as pd

import causalpy as cp

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
seed = 42

Load data

df = (
    cp.load_data("covid")
    .assign(date=lambda x: pd.to_datetime(x["date"]))
    .set_index("date")
)

treatment_time = pd.to_datetime("2020-01-01")
df.head()

	temp	deaths	year	month	t	pre
date
2006-01-01	3.8	49124	2006	1	0	True
2006-02-01	3.4	42664	2006	2	1	True
2006-03-01	3.9	49207	2006	3	2	True
2006-04-01	7.4	40645	2006	4	3	True
2006-05-01	10.7	42425	2006	5	4	True

The columns are:

• date + year: self explanatory

• month: month, numerically encoded. Needs to be treated as a categorical variable

• temp: average UK temperature (Celsius)

• t: time

• pre: boolean flag indicating pre or post intervention

Run the analysis

In this example we are going to standardize the data. So we have to be careful in how we interpret the inferred regression coefficients, and the posterior predictions will be in this standardized space.

Note

The random_seed keyword argument for the PyMC sampler is not necessary. We use it here so that the results are reproducible.

result = cp.InterruptedTimeSeries(
    df,
    treatment_time,
    formula="standardize(deaths) ~ 0 + standardize(t) + C(month) + standardize(temp)",
    model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]

fig, ax = result.plot()

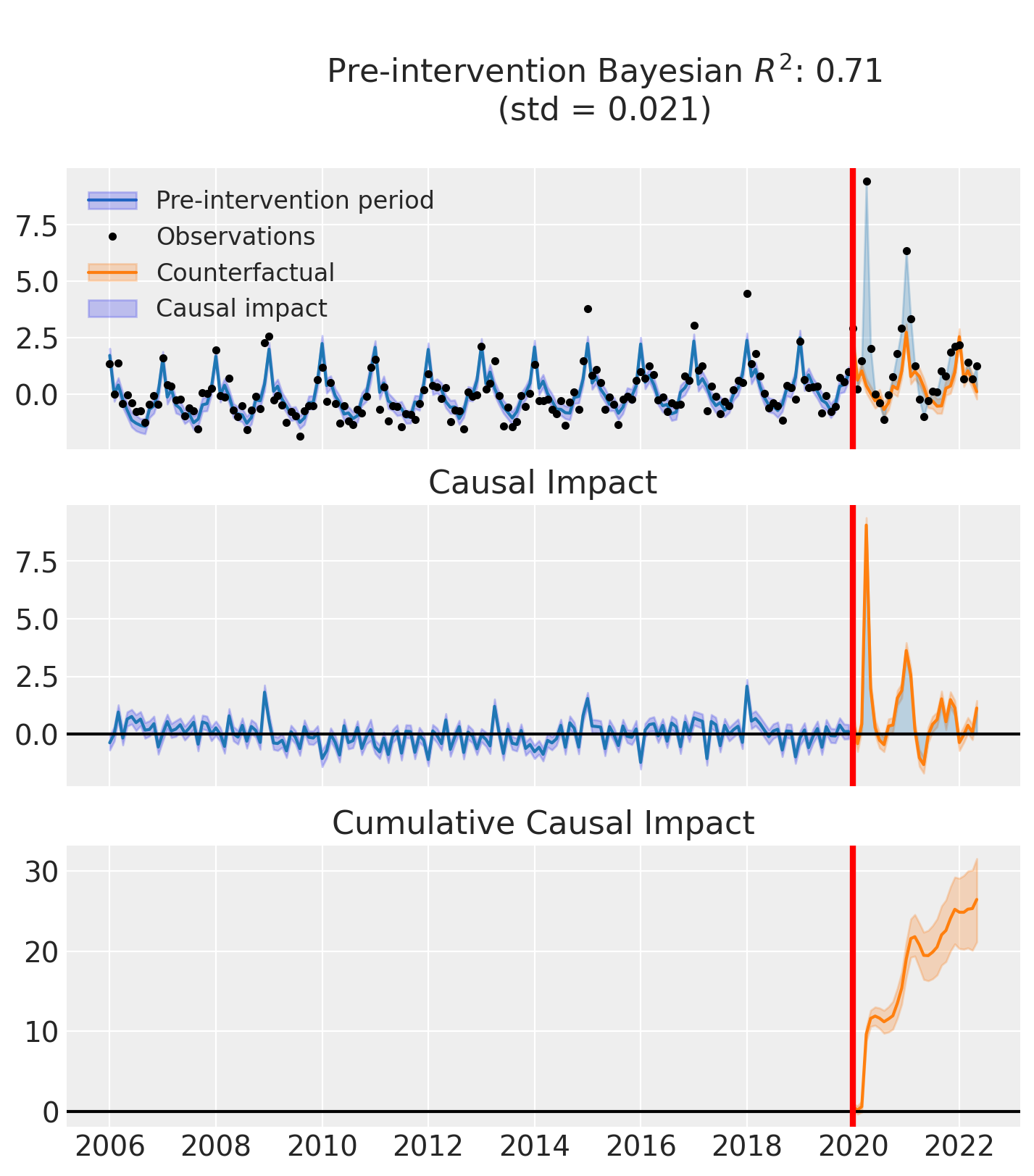
result.summary()

==================================Pre-Post Fit==================================
Formula: standardize(deaths) ~ 0 + standardize(t) + C(month) + standardize(temp)
Model coefficients:
    C(month)[1]        1.6, 94% HDI [1.1, 2]
    C(month)[2]        -0.2, 94% HDI [-0.64, 0.25]
    C(month)[3]        0.26, 94% HDI [-0.11, 0.64]
    C(month)[4]        -0.035, 94% HDI [-0.33, 0.26]
    C(month)[5]        -0.15, 94% HDI [-0.45, 0.15]
    C(month)[6]        -0.22, 94% HDI [-0.62, 0.2]
    C(month)[7]        -0.025, 94% HDI [-0.54, 0.49]
    C(month)[8]        -0.42, 94% HDI [-0.9, 0.045]
    C(month)[9]        -0.45, 94% HDI [-0.82, -0.06]
    C(month)[10]       -0.058, 94% HDI [-0.34, 0.23]
    C(month)[11]       -0.36, 94% HDI [-0.69, -0.021]
    C(month)[12]       0.076, 94% HDI [-0.34, 0.51]
    standardize(t)     0.23, 94% HDI [0.15, 0.31]
    standardize(temp)  -0.44, 94% HDI [-0.74, -0.15]
    y_hat_sigma        0.55, 94% HDI [0.5, 0.62]

Effect Summary Reporting

For decision-making, you often need a concise summary of the causal effect with key statistics. The effect_summary() method provides a decision-ready report with average and cumulative effects, HDI intervals, tail probabilities, and relative effects. This provides a comprehensive summary without manual post-processing.

Note

Note that in this example, the data has been standardized, so the effect estimates are in standardized units. When interpreting the results, keep in mind that the effects are relative to the standardized scale of the outcome variable.

# Generate effect summary for the full post-period
stats = result.effect_summary()
stats.table

	mean	median	hdi_lower	hdi_upper	p_gt_0	relative_mean	relative_hdi_lower	relative_hdi_upper
average	0.913080	0.915239	0.730235	1.107721	1.0	181.148029	85.906924	288.197309
cumulative	26.479315	26.541928	21.176827	32.123920	1.0	181.148033	85.906925	288.197316

# View the prose summary
print(stats.text)

Post-period (2020-01-01 00:00:00 to 2022-05-01 00:00:00), the average effect was 0.91 (95% HDI [0.73, 1.11]), with a posterior probability of an increase of 1.000. The cumulative effect was 26.48 (95% HDI [21.18, 32.12]); probability of an increase 1.000. Relative to the counterfactual, this equals 181.15% on average (95% HDI [85.91%, 288.20%]).

# You can also analyze a specific time window, e.g., the first 6 months of 2020
stats_window = result.effect_summary(
    window=(pd.to_datetime("2020-01-01"), pd.to_datetime("2020-06-30"))
)
stats_window.table

	mean	median	hdi_lower	hdi_upper	p_gt_0	relative_mean	relative_hdi_lower	relative_hdi_upper
average	1.986129	1.986069	1.793216	2.190517	1.0	293.850773	188.686022	418.687563
cumulative	11.916776	11.916415	10.759296	13.143105	1.0	293.850776	188.686024	418.687570