Interrupted Time Series (ITS) with scikit-learn models

This notebook shows an example of using interrupted time series, where we do not have untreated control units of a similar nature to the treated unit and we just have a single time series of observations and the predictor variables are simply time and month.

import pandas as pd
from sklearn.linear_model import LinearRegression

import causalpy as cp

%config InlineBackend.figure_format = 'retina'

Load data

df = (
    cp.load_data("its")
    .assign(date=lambda x: pd.to_datetime(x["date"]))
    .set_index("date")
)

treatment_time = pd.to_datetime("2017-01-01")
df.head()

	month	year	t	y
date
2010-01-31	1	2010	0	25.058186
2010-02-28	2	2010	1	27.189812
2010-03-31	3	2010	2	26.487551
2010-04-30	4	2010	3	31.241716
2010-05-31	5	2010	4	40.753973

Run the analysis

result = cp.InterruptedTimeSeries(
    df,
    treatment_time,
    formula="y ~ 1 + t + C(month)",
    model=LinearRegression(),
)

Examine the results

fig, ax = result.plot()

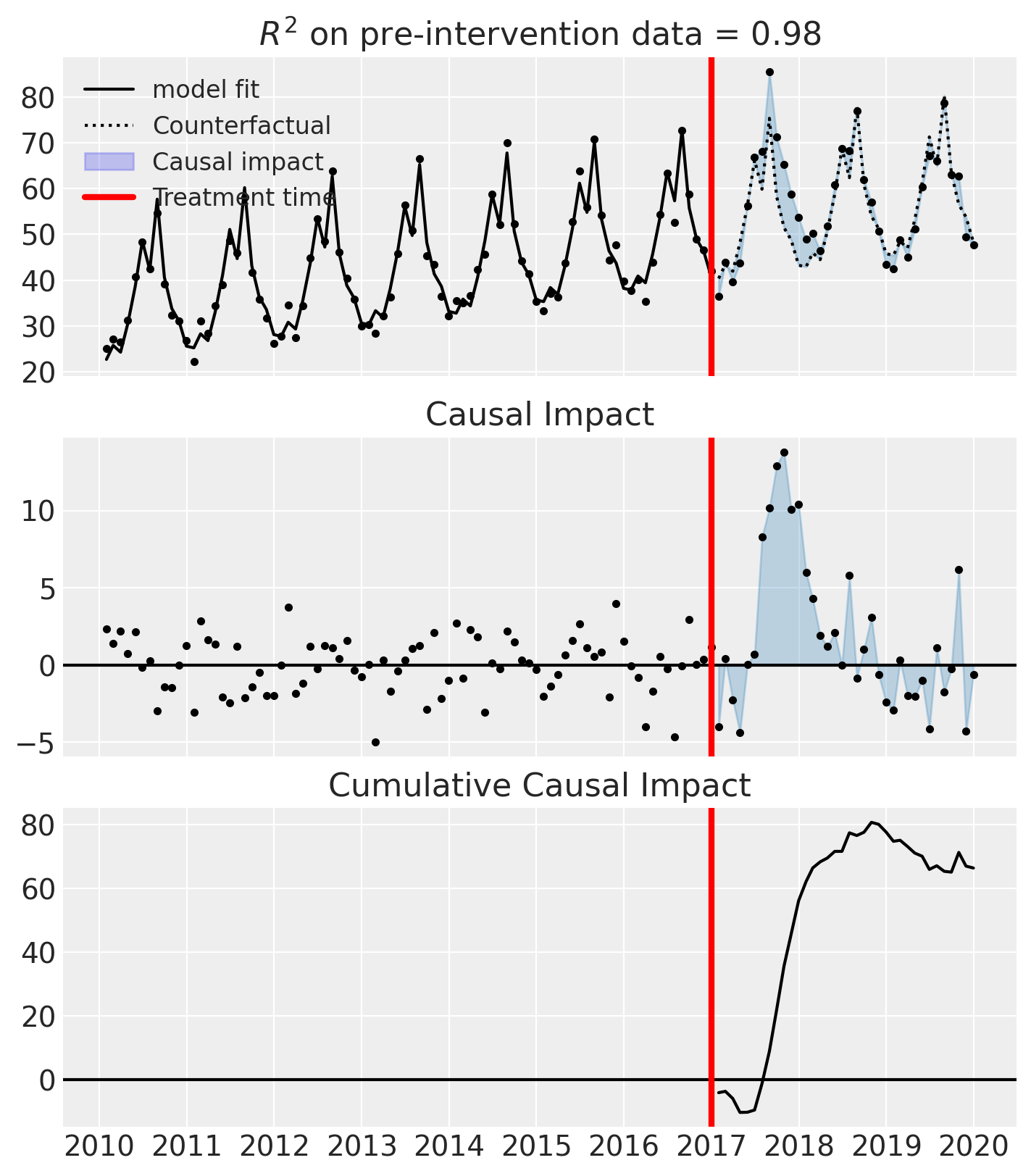
result.summary(round_to=3)

==================================Pre-Post Fit==================================
Formula: y ~ 1 + t + C(month)
Model coefficients:
  Intercept     	         0
  C(month)[T.2] 	      2.85
  C(month)[T.3] 	      1.16
  C(month)[T.4] 	      7.15
  C(month)[T.5] 	        15
  C(month)[T.6] 	      24.8
  C(month)[T.7] 	      18.2
  C(month)[T.8] 	      33.5
  C(month)[T.9] 	      16.2
  C(month)[T.10]	      9.19
  C(month)[T.11]	      6.28
  C(month)[T.12]	     0.578
  t             	      0.21

Effect Summary Reporting

For decision-making, you often need a concise summary of the causal effect. The effect_summary() method provides a decision-ready report with key statistics.

Note

OLS vs PyMC Models: When using OLS models (scikit-learn), the effect_summary() provides confidence intervals and p-values (frequentist inference), rather than the posterior distributions, HDI intervals, and tail probabilities provided by PyMC models (Bayesian inference). OLS tables include: mean, CI_lower, CI_upper, and p_value, but do not include median, tail probabilities (P(effect>0)), or ROPE probabilities.

# Generate effect summary for the full post-period
stats = result.effect_summary()
stats.table

	mean	ci_lower	ci_upper	p_value	relative_mean	relative_ci_lower	relative_ci_upper
average	1.845561	0.161437	3.529686	0.032645	3.366709	0.150601	6.582817
cumulative	66.440209	5.811718	127.068701	0.032645	121.201506	5.421618	236.981394

# View the prose summary
print(stats.text)

Post-period (2017-01-31 00:00:00 to 2019-12-31 00:00:00), the average effect was 1.85 (95% CI [0.16, 3.53]), with a p-value of 0.033. The cumulative effect was 66.44 (95% CI [5.81, 127.07]); p-value 0.033. Relative to the counterfactual, this equals 3.37% on average (95% CI [0.15%, 6.58%]).